Velocidad del sonido: Efecto Doppler

En cuanto al sonido, es el efecto por el cual el tono de un sonido emitido por una fuente que se aproxima al oyente es más agudo que si la fuente se aleja, en cuyo caso se percibiría más grave.

Se entiende sobretodo cuando oímos pasar a un vehículo con sirena (bomberos, policía).

El efecto Doppler, llamado así por el austríaco Christian Andreas Doppler, es el aparente cambio de frecuencia de una onda producido por el movimiento relativo entre la fuente, el emisor y/o el medio. Doppler propuso este efecto en 1842 en su tratado Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels (Sobre el color de la luz en estrellas binarias y otros astros).

Dicho de otra Forma, todos hemos notado que la altura (una de las características de un sonido) de la sirena de una ambulancia que se aproxima se reduce bruscamente cuando la ambulancia pasa al lado nuestro

para alejarse. Esto es lo que se llama "Efecto Doppler". El fenómeno fue descripto por primera vez por el matemático y físico austríaco Christian Doppler (1803-1853). El cambio de altura se llama en Física "desplazamiento de la frecuencia" de las ondas sonoras. Cuando la ambulancia se acerca, las ondas provenientes de la sirena se comprimen, es decir, el tamaño de las ondas disminuye, lo cual se traduce en la percepción de una frecuencia o altura mayor. Cuando la ambulancia se aleja, las ondas se separan en relación con el observador causando que la frecuencia observada sea menor que la de la fuente. (El efecto se puede ver más claramente en un applet de Walter Fendt.) Por el cambio en la altura de la sirena, se puede saber si la misma se está alejando o acercando. Si se pudiera medir la velocidad de cambio de la altura, se podría también estimar la velocidad de la ambulancia.

DICHO EN FORMULAS:

Observador acercándose a una fuente

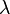Imaginemos que un observador O se mueve con una velocidad $v_{o} \,$ que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad V, frecuencia $'''f''' \,$ y longitud de onda $\lambda \,$ . Por lo tanto, la velocidad de las ondas respecto del observador no será $v \,$ , sino la siguiente:

$\ v' = v + v_{o}$

Sin embargo, no debemos olvidar que como la velocidad del medio no cambia, la longitud de onda será la misma, por lo tanto, si:

$\ v = f \cdot \lambda \Rightarrow f = \frac{v}{\lambda}$

Pero como mencionamos en la primera explicación, el observador al acercarse a la fuente oirá un sonido más agudo, esto implica que su frecuencia es mayor. A esta frecuencia mayor captada por el observador se la denomina frecuencia aparente, que la denominamos f'.

$\ f' = \frac{v'}{\lambda} = \frac{v + v_{o}}{\lambda} = \frac{v}{\lambda} + \frac{ v_{o} }{\lambda} = f + \frac{v_{o} }{\lambda} = f \cdot \bigg(1 + \frac{v_{o} }{f \cdot \lambda}\bigg) = f \cdot \bigg( 1 + \frac{v_{o} }{v}\bigg)$

El observador escuchará un sonido de mayor frecuencia debido a que 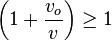$\bigg( 1 + \frac{v_{o} }{v}\bigg) \ge 1$

Observador alejándose de una fuente

Analicemos el caso contrario: cuando el observador se aleja de la fuente, la velocidad será 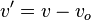$v' = v - v_{o} \,$ y de manera superior usando el teorema de pitagoras análoga podemos deducir que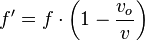 $f' = f \cdot \bigg( 1 - \frac{v_{o} }{v}\bigg)$

Fuente acercándose al observador

En este caso la frecuencia aparente percibida por el observador será mayor que la frecuencia real emitida por la fuente, lo que genera que el observador perciba un sonido más agudo.

Por tanto, la longitud de onda percibida para una fuente que se mueve con velocidad $v_{s}\,$ será:

$\mathcal \lambda ' = \lambda - \Delta \lambda$

Como $\lambda = \frac{v}{f}$ podemos deducir que:

$f' = \frac{v}{\lambda '}= \frac{v}{\lambda - \frac{v_{s} }{f}} = \frac{v}{\frac{v}{f} - \frac{v_{s} }{f}} = f \cdot \bigg(\frac{v}{v - v_{s} }\bigg)$

Fuente alejándose del observador

Haciendo un razonamiento análogo para el caso contrario: fuente alejándose; podemos concluir que la frecuencia percibida por un observador en reposo con una fuente en movimiento será:

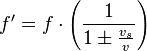
$f' = f \cdot \Bigg( \frac{1}{1 \pm \frac{v_{s}}{v}} \Bigg)$

Cuando la fuente se acerque al observador se pondrá un signo (-) en el denominador, y cuando la fuente se aleje se reemplazará por (+).

Al terminar de leer lo anteriormente expuesto surge la siguiente pregunta: ¿Qué pasará si la fuente y el observador se mueven al mismo tiempo?. En este caso particular se aplica la siguiente fórmula, que no es más que una combinación de las dos:

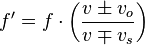
$f' = f \cdot \bigg( \frac{v \pm v_{o}}{v \mp v_{s}} \bigg)$

Los signos 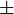$\pm$ y $\mp$ deben ser aplicados de la siguiente manera: si el numerador es una suma, el denominador debe ser una resta y viceversa.

Ejemplo

Un observador se mueve a una velocidad de 42 m/s hacia un trompetista en reposo. El trompetista está tocando (emitiendo) la nota La (440 Hz). ¿Qué frecuencia percibirá el observador, sabiendo que $\ v_{sonido} \,$ = 340 m/s

Solución: Si el observador se acerca hacia la fuente, implica que la velocidad con que percibirá cada frente de onda será mayor, por lo tanto la frecuencia aparente será mayor a la real (en reposo). Para que esto ocurra debemos aplicar el signo (+) en la ecuación.

$f' = f \cdot \bigg( 1 \pm \frac{v_{o} }{v} \bigg)$

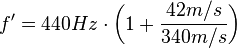
$f' = 440 Hz \cdot \bigg( 1 + \frac{42 m/s }{340 m/s} \bigg)$

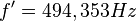
$\ f' = 494,353 Hz$

En este caso particular, el trompetista emite la nota La a 440 Hz; sin embargo, el observador percibe una nota que vibra a una frecuencia de 494,353 Hz, que es la frecuencia perteneciente a la nota Si. Musicalmente hablando, el observador percibe el sonido con un tono más agudo del que se emite realmente.

Velocidad del sonido

sábado, 11 de septiembre de 2010

Efecto Doppler